
扫码购买正式版题库
- 海量题库
- 全真模拟
- 专项训练
- 预测试题
- 押题密卷
- 错题强化

设A=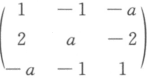 ,求A的特征值与特征向量,判断矩阵A是否可对角化,若可对角化,求出可逆矩阵P及对角阵.
,求A的特征值与特征向量,判断矩阵A是否可对角化,若可对角化,求出可逆矩阵P及对角阵.
问答题
设A=,求A的特征值与特征向量,判断矩阵A是否可对角化,若可对角化,求出可逆矩阵P及对角阵.
最新更新

热门题库
- 成考(专升本)题库
- 煤矿班组长题库
- 安全员(三类人员)题库
- 施工员题库
- P气瓶作业题库
- (中级)经济师题库
- N厂内专用机动车辆作业题库
- 电工题库
- (初级)银行从业资格题库
- 高校教师资格证题库
- 消防设施操作员题库
- 初级会计职称题库
- 高级会计题库
- 理财规划师题库
- 道路运输题库
- 环境影响评价工程师题库
- 房地产经纪人题库
- 教师招聘题库
- 一级建造师题库
- 安全员题库
- 营养师题库
- Q起重机械作业题库
- 同等学力申硕题库
- 检验类题库
- 土木工程师(水利水电)题库
- 研究生入学题库
- 消防工程师题库
- 电工作业题库
- 焊工作业题库
- A特种设备安全管理题库
- 煤矿安全管理人员题库
- 税务师题库
- 试验检测师(含助理)题库
- 统计师题库
- 建筑特殊工种题库
- 安全工程师题库
- 教师资格题库
- 理工类题库
- 安全管理人员题库
- 茶艺师题库
- 证券投资顾问题库
- 一级注册建筑师题库
- 中式烹调师题库
- 证劵从业(旧版)题库
- 会计从业资格考试题库
- 二级建造师题库
- 软件水平考试题库
- (高级)经济师题库
- 卫生类题库
- 二级注册建筑师题库
- 高处作业题库
- 会计从业题库
- 材料员题库
- 煤矿主要负责人题库
- 烟花爆竹安全作业题库
- 机械员题库
- 注册测绘师题库
- 国家电网招聘题库
- 演出经纪人题库
- 证劵从业(新版)题库
- 报关员题库
- 特种设备焊接作业题库
- 审计师题库
- T电梯作业题库
- 中级安全工程师题库
- 主治类题库
- 二级造价工程师题库
- 监管人员执法题库
- 劳务员题库
- 西式面点师题库
- 公安政法干警题库
- 汽车修理工题库
- 冶金(有色)生产安全作业题库
- BIM工程师题库
- 公用设备工程师题库
- 执业药师题库
- 投资项目管理师题库
- 招标师题库
- G锅炉作业题库
- 健康管理师题库
- 房地产经纪协理题库
- 监理工程师题库
- 注册环保工程师题库
- R压力容器作业题库
- 导游资格证题库
- 投资银行业务-保荐代表人题库
- 注册会计师题库
- 卫生招聘考试题库
- 质量工程师题库
- 银行招聘考试题库
- 报检员题库
- 期货从业资格题库
- 岩土工程师题库
- 设备监理师题库
- 物业管理师题库
- 成考(高起点)题库
- 资产评估师题库
- (初级)经济师题库
- D压力管道作业题库
- 保育员题库
- 三支一扶题库
- 自考(医学)题库
- (中级)银行从业资格题库
- 标准员题库
- 心理咨询师题库
- 注册消防工程师题库
- 注册结构工程师题库
- 资料员题库
- 车工题库
- 危险化学品安全作业题库
- 陕西省-社区专职工作人员招聘题库
- 汽车驾驶员题库
- 事业单位公开招聘题库
- 注册城乡规划师题库
- 基金从业资格题库
- 主要负责人题库
- 焊工题库
- 煤矿特种作业人员题库
- 制冷与空调作业题库
- 国家公务员题库
- 医师类题库
- 金属非金属矿山安全作业题库
- 护理类题库
- 中药学类题库
- 房地产估价师题库
- 中式面点师题库
- 中级会计职称题库
- 初级管理会计师题库
- 咨询工程师题库
- 军队文职人员招聘题库
- 证券分析师题库
- 注册电气工程师题库
- 药学类题库
- 石油天然气安全作业题库
- 一级造价工程师题库
- 法律职业资格(原司法考试)题库
- 质量员题库
- 健康管理师题库
- 企业人力资源管理师题库
- 土地登记代理人题库
- 社会工作者题库
- 综合类题库
- 省公务员-行测题库
- 钳工题库
- 美容师题库

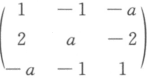 ,求A的特征值与特征向量,判断矩阵A是否可对角化,若可对角化,求出可逆矩阵P及对角阵.
,求A的特征值与特征向量,判断矩阵A是否可对角化,若可对角化,求出可逆矩阵P及对角阵.