问答题
设总体X的概率密度为f(x)=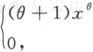 ,
,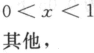 其中θ>-1是未知参数,X1,
X2,…,Xn是来自总体X的一个容量为n的简单随机样本,分别用矩估计法和最大似然估计法求参数θ的估计量.
其中θ>-1是未知参数,X1,
X2,…,Xn是来自总体X的一个容量为n的简单随机样本,分别用矩估计法和最大似然估计法求参数θ的估计量.
正确答案:A (备注:此答案有误)
相似试题
-
问答题
设二维随机变量(X,Y)服从区域G上的均匀分布,其中G是由x-y=0,x+y=2,与y=0所围成的三角形区域. (Ⅰ)求X的概率密度fx(x); (Ⅱ)求条件概率密度.
-
问答题
设随机变量X的概率密度为fx(x)=求y=e^x的概率密度FY(y).
-
单选题
设随机变量(X,Y)服从二维正态分布,且X与Y不相关,fX(x),fY(y)分别表示X,Y的概率密度,则在Y=y的条件下,X的条件概率密度fX Y(x y)为( )。
-
多选题
概率密度曲线()。
-
问答题
设总体X的概率密度为f(x)=,其中未知参数θ>0,设X1,X2,…,X是来自总体X的简单样本.(1)求θ的最大似然估计量;(2)该估计量是否是无偏估计量?说明理由.
热门题库
- 养老护理员
- 导游资格证
- 茶艺师
- 制冷工
- 注册消防工程师
- 银行招聘考试
- 高级会计
- 高校教师资格证
- 工业机器人运维员
- 房地产估价师
- 注册会计师
- 中式面点师
- 陕西省-社区专职工作人员招聘
- 软件水平考试
- 煤矿类从业人员
- 农产品食品检验员
- 保卫管理员
- 电子商务师
- 护理类
- 注册结构工程师
- 道路运输
- 机械员
- 美容师
- 健康管理师
- 消防工程师
- 标准员
- (中级)经济师
- 钳工
- 物流服务师
- (初级)经济师
- 施工员
- 卫生类
- 中药学类
- 计算机及外部设备装配调试员
- 安全员
- 理财规划师
- R压力容器作业
- 岩土工程师
- 综合类
- 焊工作业
- 企业人力资源管理师
- 餐厅服务员
- 农业技术员
- BIM工程师
- Y大型游乐设施
- 轨道交通信号工
- 医师类
- 仓库管理员
- 园林绿化工
- 初级管理会计师
- 咨询工程师
- 西式面点师
- 家畜饲养员
- 安全员(三类人员)
- 驾考科一、科四
- 教师招聘
- 保育员
- 网络安全管理员
- 注册城乡规划师
- 钢筋工
- 冶金(有色)生产安全作业
- 主治类
- 一级造价工程师
- 石油天然气安全作业
- 装饰美工
- 理工类
- 注册测绘师
- (中级)银行从业资格
- 公安政法干警
- 省公务员-行测
- 烟花爆竹安全作业
- 高处作业
- 健康管理师
- 证劵从业(新版)
- 美发师
- 投资银行业务-保荐代表人
- 卫生招聘考试
- 网络与信息安全管理员
- 车工
- 社会工作者
- 期货从业资格
- 眼镜验光员
- 焊工
- 试验检测师(含助理)
- 教师资格
- 缝纫工
- 税务师
- D压力管道作业
- 初级会计职称
- 劳务员
- 注册电气工程师
- T电梯作业
- 药学类
- 电工作业
- 新安全生产法
- 材料员
- (初级)银行从业资格
- 成考(专升本)
- 植物检疫检验员
- 二级建造师
- 证劵从业(旧版)
- 同等学力申硕
- 煤矿安全管理人员
- 国家公务员
- 审计师
- 执业药师
- 金属非金属矿山安全作业
- 报关员
- 家政服务员
- 招标师
- 土地登记代理人
- 统计师
- 无人机驾驶员
- 物业管理师
- 建筑特殊工种
- 动物检疫检验员
- 铣床
- F安全阀校验
- 税务考试题库
- G锅炉作业
- 法律职业资格(原司法考试)
- 房地产经纪协理
- 会计从业资格考试
- 成考(高起点)
- 育婴员
- 证券分析师
- 工业机器人操作员
- 园艺工
- 质量员
- 公用设备工程师
- 土木工程师(水利水电)
- 基金从业资格
- 事业单位公开招聘
- 三支一扶
- 环境影响评价工程师
- 资产评估师
- 研究生入学
- 国家电网招聘
- 煤矿特种作业人员
- 监管人员执法
- 公共营养师
- 职业道德
- 消防设施操作员
- 安全工程师
- 特种设备焊接作业
- 演出经纪人
- 一级建造师
- 会计从业
- 注册环保工程师
- 煤矿班组长
- Q起重机械作业
- 证券投资顾问
- 汽车驾驶员
- 一级注册建筑师
- (高级)经济师
- 设备监理师
- P气瓶作业
- 中级安全工程师
- 报检员
- 房地产经纪人
- 架子工
- 军队文职人员招聘
- 二级造价工程师
- 心理咨询师
- 汽车修理工
- A特种设备安全管理
- 自考(医学)
- 汽车发动机
- 危险化学品安全作业
- 中级会计职称
- 工程测量员
- 形象设计师
- 营养师
- 中式烹调师
- 质量工程师
- 监理工程师
- 砌筑工
- 投资项目管理师
- 资料员
- 主要负责人
- 二级注册建筑师
- 煤矿主要负责人
- N厂内专用机动车辆作业
- 制冷与空调作业
- 医药商品购销员
- 检验类
- 安全管理人员
- 电工
- 制油工

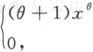 ,
,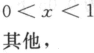 其中θ>-1是未知参数,X1,
X2,…,Xn是来自总体X的一个容量为n的简单随机样本,分别用矩估计法和最大似然估计法求参数θ的估计量.
其中θ>-1是未知参数,X1,
X2,…,Xn是来自总体X的一个容量为n的简单随机样本,分别用矩估计法和最大似然估计法求参数θ的估计量.